
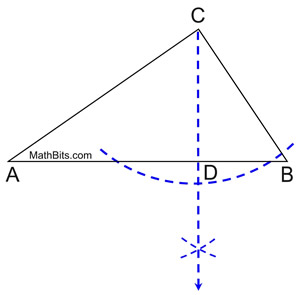
#Construction of an altitude geometry how to
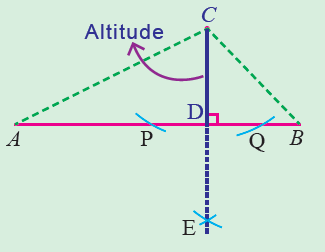
How to Find the Altitude of a TriangleĮvery triangle has three altitudes. To get the altitude for ∠ D, you must extend the side G U far past the triangle and construct the altitude far to the right of the triangle.
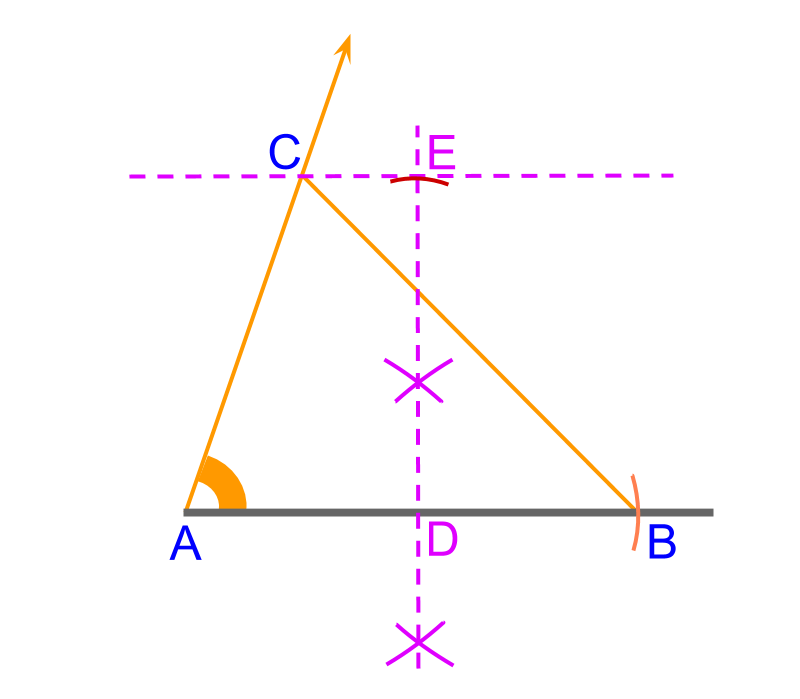
To get that altitude, you need to project a line from side D G out very far past the left of the triangle itself. The altitude from ∠ G drops down and is perpendicular to U D, but what about the altitude for ∠ U? We can construct three different altitudes, one from each vertex.įor △ G U D, no two sides are equal and one angle is greater than 90 °, so you know you have a scalene, obtuse (oblique) triangle.
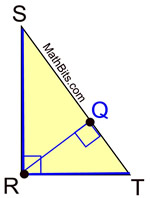
The height or altitude of a triangle depends on which base you use for a measurement. How big a rectangular box would you need? Your triangle has length, but what is its height? Imagine you ran a business making and sending out triangles, and each had to be put in a rectangular cardboard shipping carton. Obtuse triangles - One interior angle is obtuse, or greater than 90 °Īn altitude is a line drawn from a triangle's vertex down to the opposite base, so that the constructed line is perpendicular to the base.Acute triangles - All interior angles are acute, or each less than 90 °.Oblique triangles break down into two types: Right - One right angle ( 90 °) and two acute angles.Anglesīy their interior angles, triangles have other classifications: Most mathematicians agree that the classic equilateral triangle can also be considered an isosceles triangle, because an equilateral triangle has two congruent sides. Equilateral - Three sides are congruent.Scalene - No two sides are congruent (equal in length).By their sides, you can break them down like this: Sides You can classify triangles either by their sides or their angles. A triangle gets its name from its three interior angles. To find the altitude, we first need to know what kind of triangle we are dealing with. Use the Pythagorean Theorem to calculate altitudes for equilateral, isosceles, and right triangles.Construct altitudes for every type of triangle.Locate the three altitudes for every type of triangle.Recognize and name the different types of triangles based on their sides and angles.Simplified versions of the general equations are easier to remember and calculate.After working your way through this lesson and video, you will be able to: If your shape is a special triangle type, scroll down to find the height of a triangle formulas. (or area = 0.5 * a * c * sin(β) or area = 0.5 * b * c * sin(α) if you have different sides given)
Use trigonometry or another formula for the area of a triangle: Then, once you know the area, you can use the basic equation to find out what is the altitude of a triangle: It's using an equation called Heron's formula that lets you calculate the area if given sides of the triangle. area = b * h / 2, where b is a base, h - heightīut how to find the height of a triangle without area? The most popular formulas are:.Well-known equation for area of a triangle may be transformed into formula for altitude of a right triangle: The most popular one is the one using triangle area, but many other formulas exist: There are many ways to find the height of the triangle.


 0 kommentar(er)
0 kommentar(er)
